全等三角形

全等三角形

全等三角形是指兩個或多個三角形的形狀和大小完全相同，能夠通過平移、旋轉或翻轉完全重合的幾何圖形。在數學中，全等關係是一種等價關係，具有自反性、對稱性和傳遞性。

在數學表示中，全等用符號"≅"表示。若三角形ABC與三角形DEF全等，則記作△ABC≅△DEF。書寫時應注意將對應頂點按順序對齊，以便清晰看出對應關係。

全等三角形具有以下基本性質：

1. 對應邊相等：全等三角形的三對對應邊長度完全相同

2. 對應角相等：全等三角形的三對對應角度量完全相同

3. 面積相等：全等三角形的面積必然相同

4. 周長相等：全等三角形的周長必然相同

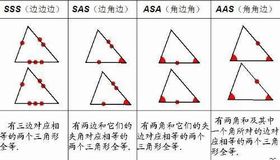
判斷兩個三角形是否全等，有以下五種基本判定方法：

邊角邊（SAS）定理

若兩個三角形的兩條邊及其夾角對應相等，則這兩個三角形全等。

角邊角（ASA）定理

若兩個三角形的兩個角及其夾邊對應相等，則這兩個三角形全等。

邊邊邊（SSS）定理

若兩個三角形的三條邊對應相等，則這兩個三角形全等。

角角邊（AAS）定理

若兩個三角形的兩個角及其中一個角的對邊對應相等，則這兩個三角形全等。

斜邊直角邊（HL）定理（僅適用於直角三角形）

若兩個直角三角形的斜邊和一條直角邊對應相等，則這兩個直角三角形全等。

不能判定全等的情況

1. 邊邊角（SSA）：當兩個三角形的兩條邊和其中一條邊的對角相等時，不能保證全等，因為可能產生兩種不同的三角形。

2. 角角角（AAA）：當兩個三角形的三個角對應相等時，只能保證相似，不能保證全等。

全等三角形在幾何學中有廣泛應用：

1. 測量：用於間接測量不可直接測量的距離或高度

2. 證明：作為證明其他幾何命題的基礎工具

3. 工程設計：在建築、機械設計等領域確保結構的對稱性和一致性

4. 圖形分析：用於分析複雜圖形的構成和性質

根據全等條件作全等三角形的方法：

1. 已知三邊（SSS）作圖

2. 已知兩邊及其夾角（SAS）作圖

3. 已知兩角及其夾邊（ASA）作圖

4. 已知兩角及一角的對邊（AAS）作圖

全等三角形的概念最早出現在古希臘數學家歐幾里得的《幾何原本》中，作為平面幾何的基礎概念之一。中國古代數學著作《九章算術》中也包含了全等三角形的應用實例。

1. 相似三角形：形狀相同但大小不一定相同的三角形

2. 等積三角形：面積相等但形狀不一定相同的三角形

3. 對稱圖形：可以通過某種變換重合的圖形

4. 剛體運動：保持圖形大小和形狀不變的幾何變換