反函數

反函數

反函數是數學中函數理論的重要概念。對於一個函數f，如果存在另一個函數g，使得對於f的定義域內的每一個x，都有g(f(x))=x，同時對於g的定義域內的每一個y，都有f(g(y))=y，那麼函數g就稱為函數f的反函數，記作f⁻¹。

並非所有函數都有反函數，反函數存在的必要條件是原函數必須是一一對應（雙射）的函數：

1. 單射性：函數必須是"一對一"的映射，即不同的輸入對應不同的輸出

2. 滿射性：函數的值域必須等於其對應域

只有同時滿足這兩個條件的函數才具有反函數。對於非一一對應的函數，可以通過限制定義域的方式使其在特定區間內具有反函數。

求一個函數的反函數通常遵循以下步驟：

1. 設原函數為y = f(x)

2. 將方程中的x和y互換位置，得到x = f(y)

3. 解這個方程，用x表示y，得到y = f⁻¹(x)

4. 確定反函數的定義域（即原函數的值域）

例如，對於函數y = 2x + 3：

1. 交換x和y：x = 2y + 3

2. 解方程：y = (x - 3)/2

3. 因此反函數為f⁻¹(x) = (x - 3)/2

反函數具有以下重要性質：

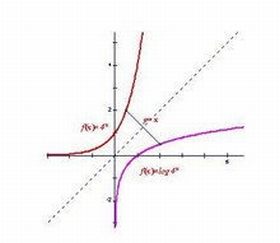
1. 對稱性：函數與其反函數的圖像關於直線y = x對稱

2. 複合性質：f(f⁻¹(x)) = x且f⁻¹(f(x)) = x

3. 單調性：如果原函數在某一區間內是嚴格單調的，則其反函數在對應區間內也是嚴格單調的

4. 導數關係：若f在x處可導且f'(x)≠0，則反函數在y=f(x)處也可導，且(f⁻¹)'(y) = 1/f'(x)

1. 線性函數：y = kx + b的反函數是y = (x - b)/k

2. 冪函數：y = xⁿ（n為正整數）的反函數是y = x^(1/n)（需限制定義域）

3. 指數函數：y = aˣ的反函數是對數函數y = logₐx

4. 三角函數：

   • y = sinx的反函數是y = arcsinx

   • y = cosx的反函數是y = arccosx

   • y = tanx的反函數是y = arctanx

5. 對數函數：y = logₐx的反函數是指數函數y = aˣ

反函數在數學和各應用領域都有廣泛應用：

1. 方程求解：通過反函數可以求解各種方程

2. 坐標變換：在幾何變換中常用反函數進行逆變換

3. 密碼學：單向函數和其反函數的概念是現代密碼學的基礎

4. 物理學：許多物理關係是可逆的，如速度與位移、壓力與體積等

5. 經濟學：需求函數與價格函數常互為反函數

反函數與複合函數有密切關係：

1. 一個函數與其反函數的複合等於恆等函數：f∘f⁻¹ = f⁻¹∘f = I

2. 兩個可逆函數的複合函數的逆函數等於各自反函數的逆向複合：(f∘g)⁻¹ = g⁻¹∘f⁻¹

3. 只有一一對應的函數在複合運算下保持可逆性

對於非一一對應的函數，可以考慮其多值反函數：

1. 如y = x²的反關係是x = ±√y，這是一個多值對應

2. 在複變函數中，反函數常表現為多值函數

3. 為避免多值性，通常限制定義域或選擇主值分支

從幾何角度看：

1. 反函數表示原函數圖像關於直線y=x的鏡像

2. 反函數的導數與原函數導數互為倒數（考慮斜率）

3. 極坐標下某些函數與其反函數可能具有相同的圖像

對於多元函數，反函數的概念推廣為反函數定理：

1. 反函數定理給出了雅可比行列式非零時局部存在反函數的條件

2. 隱函數定理是反函數定理的推廣

3. 在高維情況下，反函數通常難以顯式表示，但可以證明其存在性和可微性