對數
對數的定義
 對數
對數對數(Logarithm)是一種數學運算,用來表示某個數(真數)是另一個數(底數)的多少次方。對數的定義如下:
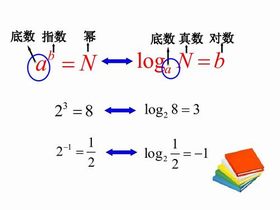
如果 (其中 , , ),則 稱為以 為底 的對數,記作:
其中:
稱為底數
稱為真數
稱為對數值
對數的歷史
對數的概念最早由蘇格蘭數學家約翰·納皮爾(John Napier)在1614年提出,目的是簡化複雜的乘除運算,使其轉化為加減運算,從而提高計算效率。後來,英國數學家亨利·布里格斯(Henry Briggs)進一步發展了常用對數(以10為底),並編制了對數表,廣泛應用於天文學、航海和工程計算。
常見的對數類型
(1) 常用對數(以10為底)
常用對數的底數為10,記作 或簡寫為 ,廣泛應用於科學計算和工程領域。
(2) 自然對數(以e為底)
自然對數的底數為自然常數 (約等於2.71828),記作 或 ,在微積分、概率統計等高等數學中非常重要。
(3) 二進制對數(以2為底)
二進制對數的底數為2,記作 ,主要應用於計算機科學和資訊理論,例如分析演算法的時間複雜度。
對數的基本性質
對數具有以下重要性質,可用於簡化計算:
乘法轉加法:
除法轉減法:
冪運算轉乘法:
換底公式:
對數的倒數關係:
對數函數及其圖像
對數函數是指形如 (, )的函數,其圖像特點如下:
定義域:
值域:全體實數
單調性:
當 時,函數單調遞增
當 時,函數單調遞減
特殊點:
(因為 )
(因為 )
對數的應用
對數在科學、工程和經濟等領域有廣泛應用,例如:
天文學:簡化大數計算
化學:計算pH值()
經濟學:計算複利和指數增長
計算機科學:分析演算法複雜度(如 )
信號處理:分貝(dB)的計算
對數與指數的關係
對數與指數是互逆運算,即:
這一性質使得對數可以用於求解指數方程,例如:
對數表的發展與現代計算
早期科學家依賴對數表進行計算,但隨著計算機和計算器的普及,對數表已逐漸被取代。現代計算可直接使用計算工具(如程式語言中的 log() 和 ln() 函數)進行高效運算。
總結
對數是一種強大的數學工具,能夠將複雜的乘除、冪運算轉化為簡單的加減法,在科學、工程和計算領域發揮重要作用。理解對數的定義、性質和應用,有助於更高效地解決實際問題。
附件列表
詞條內容僅供參考,如果您需要解決具體問題
(尤其在法律、醫學等領域),建議您咨詢相關領域專業人士。
上一篇 審計(獨立性的經濟監督活動) 下一篇 市盈率
