歐拉公式

歐拉公式

歐拉公式（Euler's formula）是數學中最重要的公式之一，由瑞士數學家萊昂哈德·歐拉（Leonhard Euler）在18世紀提出。這個公式建立了複數指數函數與三角函數之間的深刻聯繫，被譽為"數學中的鑽石"。

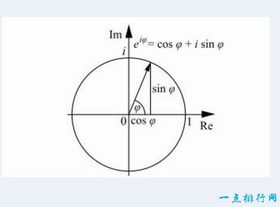
歐拉公式的基本形式為：e^(ix) = cos x + i sin x

其中：

• e 是自然對數的底（約等於2.71828...）

• i 是虛數單位，滿足 i² = -1

• x 是以弧度為單位的實數變量

當x = π時，公式變為著名的歐拉恆等式：e^(iπ) + 1 = 0

歐拉公式的發展歷程：

• 1714年，英國數學家羅傑·科茨（Roger Cotes）首次發現了類似關係

• 1740年，歐拉在給約翰·伯努利的信中提到了這個公式

• 1748年，歐拉在其著作《無窮小分析引論》中正式發表了這個公式

• 後來經過多位數學家的完善，成為現代形式

歐拉公式有多種證明方法，以下是幾種常見的證明途徑：

泰勒級數展開法

利用函數的泰勒級數展開：

• e^x = 1 + x + x²/2! + x³/3! + ...

• sin x = x - x³/3! + x⁵/5! - ...

• cos x = 1 - x²/2! + x⁴/4! - ...

將ix代入e^x的展開式，整理後即可得到歐拉公式。

微分方程法

考慮函數f(x) = e^(-ix)(cos x + i sin x)，通過求導可證明f'(x) = 0，即f(x)為常數，再代入x=0即可得證。

極限法

利用複數指數的極限定義：(1 + ix/n)^n當n→∞時的極限。

歐拉公式在複平面上有直觀的幾何意義：

• 複數e^(ix)表示單位圓上角度為x的點

• 實部對應cos x，虛部對應sin x

• 隨著x的變化，點沿單位圓勻速旋轉

當x = π時，歐拉公式變為：e^(iπ) = -1或e^(iπ) + 1 = 0

這個等式被稱為"數學中最優美的公式"，因為它將五個最重要的數學常數（0,1,e,i,π）用一個簡單的等式聯繫起來。

歐拉公式在數學和物理的多個領域有廣泛應用：

複變函數論

• 建立了指數函數與三角函數的聯繫

• 是複數運算的基礎工具

信號處理

• 傅里葉變換的核心數學基礎

• 簡化了波動和振動的分析

量子力學

• 薛定諤方程的解常涉及歐拉公式

• 波函數的相位因子表示

電路分析

• 交流電路分析中的相量法

• 阻抗計算的基礎

歐拉公式有多種推廣形式：

多複數情況

對於任意複數z = a + ib：e^z = e^a(cos b + i sin b)

矩陣指數

對於某些矩陣A，有類似的指數映射：e^A = I + A + A²/2! + A³/3! + ...

四元數情況

對於單位四元數，也有類似的指數表示法。

歐拉公式的重要性體現在：

1. 統一了指數函數與三角函數

2. 提供了複數運算的強大工具

3. 簡化了許多數學和物理問題的求解

4. 揭示了數學不同分支之間的深刻聯繫

5. 成為現代科學技術的基礎數學工具之一

歐拉公式不僅是數學上的重要成果，也是人類智慧的結晶，展現了數學之美的極致。