斐波那契數列

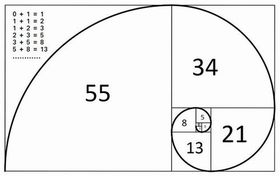斐波那契數列

斐波那契數列（Fibonacci sequence），又稱黃金分割數列，是一個經典的數學序列。其定義如下：

• F₀ = 0

• F₁ = 1

• Fₙ = Fₙ₋₁ + Fₙ₋₂（當n≥2時）

斐波那契數列最早出現在印度數學中，但由意大利數學家列昂納多·斐波那契（Leonardo Fibonacci）在1202年出版的《計算之書》中引入歐洲。該書提出著名的"兔子繁殖問題"，奠定了此數列的研究基礎。

斐波那契數列具有以下數學特性：

1. 遞歸關係：每個數字都是前兩個數字的和

2. 與黃金比例關係：相鄰兩數比值趨近於黃金比例(1.618...)

3. 封閉形式表達式：可用比奈公式直接計算任意項

4. 加法恆等式：多種數學恆等式成立

斐波那契數列在數學領域有廣泛應用：

• 數論研究

• 組合數學

• 遞歸算法分析

• 矩陣理論

• 連分數研究

該數列在自然界中隨處可見：

1. 植物學：葉序排列、花瓣數量

2. 生物生長：鸚鵡螺殼螺旋

3. 晶體結構：某些準晶體排列

4. 星系結構：螺旋星系旋臂

斐波那契數列影響多種藝術形式：

• 繪畫構圖：達文西作品比例

• 建築設計：帕特農神廟比例

• 音樂創作：某些曲式結構

• 攝影構圖：黃金分割構圖法

數學家發展了多種變體：

1. 盧卡斯數列

2. 斐波那契多項式

3. 隨機斐波那契序列

4. 負數項擴展

常見計算方法包括：

• 遞歸算法（效率低）

• 迭代算法（效率高）

• 矩陣快速冪法（最優）

• 比奈公式直接計算

關於斐波那契數列仍存在開放問題：

• 素數分布規律

• 與其他數列的深層關係

• 在高維空間的推廣形式

• 在量子物理中的潛在應用

斐波那契數列已成為流行文化元素：

• 《達文西密碼》等文學作品

• 多部科幻電影情節

• 金融市場技術分析工具

• 遊戲設計中的平衡機制

此數列因其簡潔定義與豐富內涵，被譽為"數學中的鑽石"，持續吸引著數學愛好者與專業研究者的探索。